Identifizierung der Entwicklung von Ermüdungsschäden in Edelstahl 316L (W.-Nr. 1.4404) durch Schallemissionsanalyse und digitale Bildkorrelation
Deutsche Übersetzung von Stephan Kallee<1> der englischen Veröffentlichung von Farhan Tanvir<2><3>*, Tariq Sattar<2>, David Mba<4>, Graham Edwards<5>, Elvin Eren<5> und Yoann Lage<6>: Identification of fatigue damage evolution in 316L stainless steel using acoustic emission and digital image correlation
<1> AluStir, Im Unterdorf 19, 63826 Geiselbach, Germany
<2> London South Bank University, 103 Borough Rd, London SE1 0AA, UK
<3> National Structural Integrity Research Centre, TWI Ltd, Granta Park, Cambridge CB21 6AL, UK
<4> De Montfort University, Gateway House, Leicester LE1 9BH, UK
<5> TWI Ltd., Granta Park, Great Abington, Cambridge CB21 6AL, UK
<6> Mistras Group Ltd, Norman Way, Over, Cambridge CB24 5QE, UK
*Korrespondierende Autor: Farhan Tanvir
MATEC Web of Conferences 165, 22007 (2018)
Zusammenfassung
Eines der Hauptziele der Überwachung der Schallemission (Acoustic Emission, AE) ist es, das sich nähernde kritische Stadium der Strukturschädigung zu identifizieren, bevor die Struktur versagt. Moderne Schallemissionanalysen werden an den Signalen im Zeit- und Frequenzbereich durchgeführt. Viele Funktionen wie Frequenz, Dauer, Anstiegszeit, Anzahl und Energie sind abhängig von den Erfassungseinstellungen, Schwellen- und Zeitparametern. Falsche Aufnahmeeinstellungen können zu einer ungenauen Klassifizierung der Schallemissionquelle führen. Diese Arbeit zeigt, dass sich ein neues Merkmal im zeitabhängigen Signal aufgrund der Renyi-Entropie 2. Ordnung als effizient bei der Identifizierung der verschiedenen Phasen des Schadens zeigt. Die Renyi-Entropie ist ein Maß für die Unsicherheit oder Zufälligkeit der Signale und wird direkt aus der Verteilung der Signalamplitude abgeleitet. Daher ist sie unabhängig von Schwellen- und Zeitparametern. Die Gültigkeit des vorgeschlagenen Parameters wird durch die Durchführung einer Schallemissionsüberwachung während des Ermüdungs-Dauerlauftests von Edelstahl 316L untersucht. Digitale Bildkorrelation und globale Dehnungsüberwachung wurden durchgeführt, um Sachschäden mit Schallemissionsaktivität in Verbindung zu bringen. Das Ergebnis zeigt, dass die Renyi-Entropie eine effektive Maßnahme ist, um kritische Phasen von Schäden im Material zu identifizieren.
Nomenklatur
- Schallemissionsanalyse (Acoustic Emission Analysis) erlaubt Rückschlüsse auf die strukturelle Integrität des Werkstoffs bzw. des Bauteils, da Risse oder Gefügeveränderungen zur Emission von Schall führen.
- Digitale Bildkorrelation (Digital Image Correlation) ist ein kamerabasiertes Verfahren zur berührungslosen Verformungsmessung. Es wird überwiegend zur Materialprüfung und zur Überwachung von mechanischen Komponenten eingesetzt.
1. Einleitung
- Stufe 1: Ermüdungsrissinitiierung
- Stufe 2: langsamer Ermüdungsrissfortschritt
- Stufe 3: schneller Rissfortschritt
2. Methodik
2.1 Experimentelle Vorgehensweise
Für die Tests wurden Hundeknochen-förmige Zugproben aus rostfreiem Edelstahl 316L (Werkstoff-Nummer 1.4404) nach der Norm E466-15, verwendet (Bild 2). Die Tabellen 1 und 2 zeigen die chemische Zusammensetzung und die mechanischen Eigenschaften des Prüflings.
E-Modul
Streckgrenze in Längsrichtung (Rp 0,1)
Zugfestigkeit in Längsrichtung
193 GPa
347 MPa
612 MPa
Tabelle 2: Mechanische Eigenschaften des Edelstahls 316L (Werkstoff-Nummer 1.4404)
Ermüdungsdauerprüfungen am Prüfling wurden mit einer servo-hydraulischen Instron-Prüfmaschine bei Umgebungstemperatur durchgeführt. Der Prüfling wurde unter sinusförmiger zyklischer Belastung geprüft, mit einer konstanten Frequenz von 5Hz, einer Spitzenlast von 24kN und Belastungsverhältnis von 0,1.
Die Schallemissionssignale aus dem Ermüdungstest wurden mit einem AMSY-6 Datenerfassungssystem aufgezeichnet und analysiert, das von der Vallen-Software gesteuert wird. Es wurden zwei Schallemissionssensoren mit einer Spitzenempfindlichkeitsfrequenz zwischen 100 kHz und 450 kHz sowie ein Vorverstärker mit einer Verstärkung von 34dB eingesetzt. Der Abstand zwischen den Sensoren für den Test betrug 90mm. Als Einstellungen für die Datenerfassung wurden eine Hit Definition Time (HDT) von 400μs, eine Re-Arm-Time von 1ms und ein Schwellenwert von 40dB verwendet. Für den Test wurde dauerbasiertes Transient Recording (TR) mit einer maximalen TR-Seitenlänge von 26,214 μs verwendet. Für die lineare 1D-Lokalisierung wurde ein 1D-Ortungsprozessor mit einer Wellengeschwindigkeitskalibrierung von 5000m/s verwendet. Die Lokalisierung erleichtert die Beseitigung des Rauschens, das durch den Kontakt von Metall zu Metall am Spannfutter entsteht, indem sie Signale aufzeichnet, die nur im Messabschnitt des Prüflings erzeugt werden.
Um die Materialantwort mit der Schallemissionsaktivität in Beziehung zu setzen, wurde der Prüfling gleichzeitig mit anderen ZfP-Techniken überwacht. Insgesamt wurden zwei Tests durchgeführt. Der erste Test wurde mit gleichzeitiger Schallemissions- und globaler Dehnungsmessung durchgeführt. Der zweite Test wurde mit gleichzeitiger Schallemissions-, Globaldehnungs- und digitaler Bildkorrelatur-Messung durchgeführt. Um die digitale Bildkorrelatur-Messung durchzuführen, wurden Pixelblöcke in den Messbereich der Probe auf der Seite der Probe gegenüber den Schallemissions-Sensoren eingeführt. Zur Erfassung des 2D-Verschiebungsfeldes der Pixelblöcke wurde ein digitales ARAMIS-5m Bildkorrelatur-System mit einer Bildrate von 15Hz bis 29Hz und einer Kameraauflösung von 2448 x 2050 px verwendet. Die Frequenz der vom Bildkorrelatur-System aufgenommenen digitalen Bilder betrug 0,005Hz.
3. Materialien und Methoden
In den 1950er Jahren führte Alfred Renyi eine parametrische Familie der Informationstheorie namens Renyi-Entropie ein, die die Shannon-Entropie generalisiert[13]. Renyi wies darauf hin, dass Shannons Entropie-Schätzung auf der ersten Funktionsklasse basiert, nämlich dem linearen Mittelungsoperator (𝑔(𝑥)=𝑐𝑥). Er schlug eine Entropieformulierung vor, die auf der zweiten Funktionsklasse, dem sogenannten nichtlinearen Mittelungsoperator (𝑔(𝑥)=𝑐2(1-𝑎)𝑥)) basiert, die sich als flexibler erwies als die Shannons Formel [14].
Die Entropie basiert auf dem Maß der Unsicherheit in einer Wahrscheinlichkeitsverteilungsfunktion und wird in Mathematik und Physik weit verbreitet [15]. Bei einer zufälligen Sequenz {𝑥1, 𝑥2, 𝑥3, … ,𝑥𝑛} wird die Renyi-Entropie, wie folgt, nach Gleichung (1) berechnet:
(1)
Log zur Basis 2 wird in diesem Fall verwendet, um die Entropie in Bits zu messen. Log zur Basis 10 oder loge kann auch verwendet werden, um die Entropie in Bins bzw. Bans zu messen. Der Einfachheit halber wird die Renyi-Entropie in diesem Beitrag als Schallemissions-Entropie bezeichnet. Der Hauptgrund für die Verwendung der Schallemissions-Entropie ist die Unabhängigkeit von Akquisitionseinstellungen wie Schwellenwert und Timing, im Gegensatz zu herkömmlichen Schallemissions-Parametern.
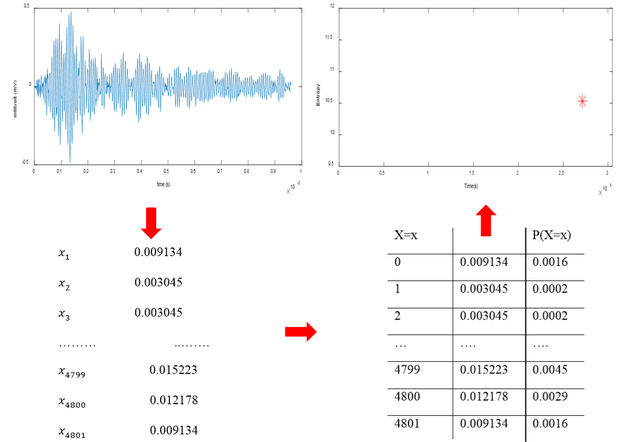
Das Berechnungsverfahren der Schallemissions-Entropie beginnt mit der Aufzeichnung der Schallemissions-Wellenform, die aus dem Experiment mit dem Schallemissions-Monitoring-System erzeugt wurde. Die aus dem Experiment aufgenommene Wellenform wird in eine txt-Datei mit Millivolt- und Mikrosekundenwerten umgewandelt. Anschließend wird die diskrete Wahrscheinlichkeitsverteilung der Wellenform berechnet. Mehrere Methoden wurden vorgeschlagen, um die Wahrscheinlichkeit der Masse zu berechnen, um die Entropie einer digitalen Wellenform zu berechnen[16][17]. Die Wahrscheinlichkeit der Massenberechnung in dieser Arbeit basiert auf der Berücksichtigung des ursprünglichen Spektrums des Signals, wie in [16] erläutert. Die Wahrscheinlichkeit der Masse für die Berechnung der Entropie, unter Berücksichtigung des ursprünglichen Spektrums des Signals wurde in der Signalverarbeitung weit verbreitet [18][19]. Nach der Wahrscheinlichkeit einer Massenberechnung wird die Schallemissions-Entropie mit Äquivalent 1 berechnet. Bild 3 zeigt die Schritte zur Berechnung der Schallemissions-Entropie.
3. Ergebnisse und Diskussion
3.1. Schallemissions-Datenerfassung mit prozentualer Verlängerung der Probe
Ein Diagramm der Spitzenamplitude der Schallemissions-Wellenform und der prozentualen Dehnung der Probe über die Zeit wurde während der zyklischen Belastung der Prüfmaschine aufgezeichnet (Bild 4). Der erste Teil der Prüfung geht einher mit einer signifikanten Erhöhung der Spitzenamplitude (bis zu 92dB) des Signals und der prozentualen Dehnung des Prüflings. In dieser Phase der Prüfung werden Signale im unteren Amplitudenbereich mit der elastischen in plastische Umwandlung des Materials[20][21] assoziiert, während Signale im höheren Amplitudenbereich (über 60dB) von anfänglichem Metall- zu Metallkontaktgeräusch[22] ausgehen können. Anschließend beginnen Signale mit geringerer Amplitude (unter 55dB) bis zu etwa 14.000s zu erscheinen. Die Zeit ab dem Beginn der Belastung bis 14.000 s kann als die Schadensakkumulations- oder Risskeimbildungsstufe betrachtet werden.
Bild 4: Schallemissions-Spitzen-Amplitude und prozentuale Verlängerung über der Zeit (das Bild wurde teilweise retuschiert, da es im englischen Original wegen eines Formatierungsfehlers unvollständig wiedergegeben wurde)
© Farhan Tanvir et al, CC BY 4.0
In Bild 5, einem Diagramm der Zählrate und der prozentualen Dehnung über der Zeit, ist zu beobachten, dass bis zu 14.000 s, mit Ausnahme des Beginns der Belastung, eine niedrige Zählrate vorliegt, was darauf hindeutet, dass es in diesem Stadium zu einer Schadensakkumulation oder einer Rissbildung kommt[23][24]. Der anfängliche Anstieg der Zählrate zu Beginn der Belastung ist auf die erhöhte mikrostrukturelle Aktivität durch elastische bis plastische Umwandlung und Lärm durch den Ladezug zurückzuführen. Am Ende dieser Phase wird der Schaden lokalisiert, es entstehen Mikrorisse und es entstehen die kurzen Risse[24]. Bild 5 zeigt auch einen plötzlichen Anstieg der Zählrate der Signale nach 14.000s. Die Erhöhung der Zählrate ist hier mit Mikroschäden des Materials wie Wachstum und Koaleszenz von Mikrorissen verbunden[24]. Durch den Vergleich mit Abbildung 4 geht eine Erhöhung der Zählfrequenz auch mit hochamplitudenhaften Signalen bei 14.000s und 18.000s (über 55dB) als Folge der Mikroschäden im Material einher.
Nach 25.000 s wird der Schaden sichtbar lokalisiert und sowohl die Zählfrequenz als auch die Spitzenamplitude nehmen aufgrund der Einleitung von Makro-Ermüdungsrissen, des Wachstums und des endgültigen Versagens signifikant zu. Die Spitzenamplitude des Signals ist ein nützlicher Parameter zur Identifizierung von Schadensmechanismen in einem Material. Allerdings ist es in diesem Experiment schwierig, Schadensmechanismen wie das Wachstum und die Koaleszenz von Mikrorissen allein durch die Beobachtung der Spitzenamplitude genau zu identifizieren, da es möglich ist, den anfänglichen Sprung in der Spitzenamplitude zu Beginn der Belastung mit dem materiellen Schaden zu verwechseln.
Bild 5: Schallemissions-Anzahl und prozentuale Verlängerung über der Zeit (das Bild wurde teilweise retuschiert, da es im englischen Original wegen eines Formatierungsfehlers unvollständig wiedergegeben wurde)
© Farhan Tanvir et al, CC BY 4.0
Als Alternative zum Spitzenamplitudenparameter wurde aus den aufgezeichneten Wellenformen ein schwellenunabhängiger Parameter namens Schallemissions-Entropie berechnet, wie in Abschnitt 1 erläutert. Die Darstellung der Schallemissions-Entropie und der prozentualen Dehnung über der Zeit ist in Bild 6 dargestellt.
Aus Bild 6 ist ersichtlich, dass die Wellenform mit höherer Spitzenamplitude zu Beginn des Tests einem niedrigeren Wert der Schallemissions-Entropie zugeordnet ist (unter 11). Während der Phase der Schadensakkumulation, bis zu 14.000 s, stellte sich die Entropievariation als stabil heraus. Die Wellenform, die bei 14.000 s aufgenommen wurde, zeigte einen plötzlichen Anstieg der Schallemissions-Entropie, höher als zu Beginn, der durch elastische zu plastische Umwandlung und mechanisches Rauschen verursacht wurde. Der plötzliche Anstieg der Schallemissions-Entropie nach 14.000 s geht auch mit einem plötzlichen Anstieg der Zählrate des Signals einher, der in Bild 5 beobachtet wurde, was darauf hindeutet, dass diese Signale aus einer erhöhten mikrostrukturellen Aktivität stammen, wie beispielsweise Wachstum und Koaleszenz von Mikrorissen[23][24]. Wellenformen, die um 18.000 s aufgenommen wurden, zeigten ebenfalls eine Zunahme der Schallemissions-Entropie bei gleichzeitiger starker Zunahme der Zählrate. Allerdings ist der Anstieg der Schallemissions-Entropie bei 18.000 s im Vergleich zur Schallemissions-Entropie bei 14.000 s nicht sehr signifikant. Dies könnte auf eine geringe Größe von Mikroschäden im Vergleich zu 14.000 s zurückzuführen sein. Die Schallemissions-Entropie war bis 23.000 s stabil. Bei etwa 25.000 s war der Schaden im Prüfling sichtbar lokalisiert und ging einher mit einem signifikanten Anstieg sowohl der Zählrate als auch der Schallemissions-Entropie des Signals, was zu der Einleitung von Makro-Ermüdungsrissen, dem Wachstum und dem endgültigen Versagen der Probe führte. Eine signifikante Anzahl von Signalen nach 25.000 s war mit einer Schallemissions-Entropie verbunden, die höher war als die Entropie zu Beginn der zyklischen Belastung.
Bild 6: Schallemissions-Entropie und prozentuale Verlängerung über der Zeit
© Farhan Tanvir et al, CC BY 4.0
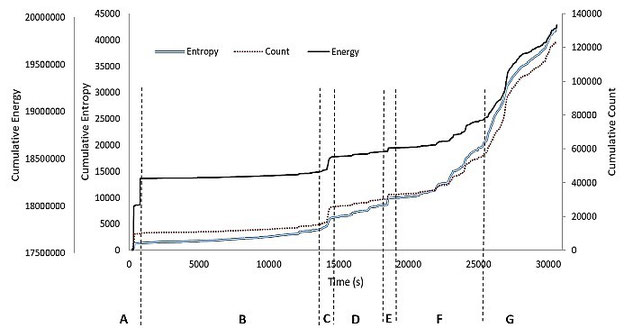
Bild 7 veranschaulicht einen Vergleich von kumulativer Anzahl, kumulativer Energie und kumulativer Entropie über die gesamte Länge des Tests. Kumulative Energie und Anzahl wurden bei der Bewertung von Ermüdungsschäden während der Schallemissions-Überwachung weit verbreitet[6][20][25][25] verwendet. Daher wurden diese Parameter ausgewählt, um den kumulativen Trend der Schallemissions-Entropie zu vergleichen. In Bild 7 ist ersichtlich, dass alle drei Kurven den gleichen Trend aufweisen. Der anfängliche Anstieg der kumulativen Parameter im Bereich A ist auf die elastisch-plastische Umwandlung und das mechanische Rauschen zurückzuführen. Region B ist die Schadensakkumulationsstufe und geht mit einem sehr geringen Anstieg der kumulativen Parameter einher. Ein plötzlicher Anstieg der kumulativen Parameter in den Regionen C und E ist auf das Wachstum und die Koaleszenz von Mikrorissen zurückzuführen. Die Regionen D und F sind mit einem stabilen Anstieg der kumulativen Parameter verbunden. Der stabile Anstieg der kumulativen Parameter ist mit einer stabilen Akkumulation von Mikroschäden wie z.B. Mikrorisswachstum verbunden. Die Region G ist von einem signifikanten Anstieg der kumulativen Parameter begleitet. Der starke Anstieg der kumulativen Parameter in der Region G von 25.000 bis 27.000 s ist auf die in[6][7][25] vorgeschlagene Makro-Ermüdungsrissinitiierung zurückzuführen und der stabile Anstieg der kumulativen Parameter von 27.000 bis 29.500 s ist mit einem stabilen Makro-Ermüdungsrisswachstum verbunden. Der starke Anstieg der kumulativen Parameter nach 29.500 s bis zum Ende ist auf das Ergebnis der schnellen Rissausbreitung, vorgeschlagen in[6][7][25].
Bild 7: Kumulative Entropie, kumulative Energie und kumulative Anzahl über die Zeit
© Farhan Tanvir et al, CC BY 4.0
Der ähnlich steigende Trend in allen drei Parametern zeigte, dass die kumulative Entropie auch als Bewertungsparameter für Ermüdungsschäden anstelle von kumulativer Anzahl und kumulativer Energie verwendet werden kann. Die obige Analyse zeigt, dass die Schallemissions-Entropie empfindlich auf die Bewertung von Ermüdungsschäden in Edelstahl 316L (Werkstoff-Nummer 1.4404) reagiert. Die Verteilung der hohen Spitzenamplitude des Signals zu Beginn des Tests war mit einem niedrigeren Wert der Schallemissions-Entropie verbunden. Materialschäden wie Wachstum und Koaleszenz von Mikrorissen, Makro-Ermüdungsrissen, Ausbreitung und letztendliches Versagen wurden von einer signifikanten Zunahme der Schallemisions-Entropie begleitet. Da die Schallemissions-Entropie ein Maß für die Unsicherheit oder Zufälligkeit in einer Wellenform ist, deutet dies darauf hin, dass die Wellenform von materiellen Schäden mit mehr Unsicherheit oder Zufälligkeit verbunden ist als die von Rauschen. Darüber hinaus zeigte die kumulative Entropie einen ähnlichen Trend wie die kumulative Anzahl und die kumulative Energie, was darauf hindeutet, dass die kumulative Entropie auch als Bewertungsparameter für Fatigue-Schäden verwendet werden kann.
3.2. Schallemissions-Datenerhebung mit digitaler Bildkorrelation
Die im ersten Test verwendete sekundäre Überwachungstechnik war die prozentuale Dehnung des Materials, die bis auf den Beginn der Belastung und den endgültigen Ausfall keine Trendwende bei der Bewertung von Ermüdungsschäden zeigte. Um die Leistung der sekundären Überwachungstechnik zu verbessern, wurde der zweite Test mit digitaler Bildkorrelations-Messung neben der Schallemissions-Überwachung durchgeführt.
Die digitale
Bildkorrelation lieferte ein vollflächiges Verschiebungs- und Dehnungsbild über die gesamte Messlänge der Probe. Es wurden mehrere Bilder während des Tests aufgenommen. Abbildung 8 zeigt
einige der Bilder, die von der digitalen
Bildkorrelation während der zyklischen Belastung der Probe aufgenommen wurden. Das Bild (a) in Figur 8 ist das Referenzbild. Dieses Bild wurde vor dem Laden der Probe aufgenommen. Das Bild
(b) wurde um 11.188 s nach Beginn des Tests aufgenommen. Das Bild (c) wurde mit 18.664 Bildern aufgenommen. In Bild (c) ist zu sehen, dass die Makrodehnung in einem kleinen Volumen lokalisiert
ist, markiert durch den schwarzen Pfeil. Lokalisierte Makrodehnungen treten lange nach der Akkumulation von Mikrorissinitiierung, Koaleszenz und Wachstum im Persistenz-Slip-Band auf. In Bild (d)
und (e) kann bei 18.665 s und 19.004 s die Ausbreitung von Makroermüdungsrissen anhand der lokalisierten Makrodehnung unter (c) identifiziert werden. Bild (f) bei 19.400 s zeigt den
endgültigen Versagen der von der digitalen
Bildkorrelation erfassten Probe. Die
digitale
Bildkorrelation liefert wichtige Informationen zur Bewertung von Ermüdungsschäden. Erstens werden Informationen über die Makrodehnungslokalisation erhalten, da die Mikroermüdungsrisse
initiiert werden, die Koaleszenz und das Wachstum. Zweitens werden Informationen über die Ausbreitung von Makro-Ermüdungsrissen gewonnen, die zum endgültigen Versagen der Probe führen.
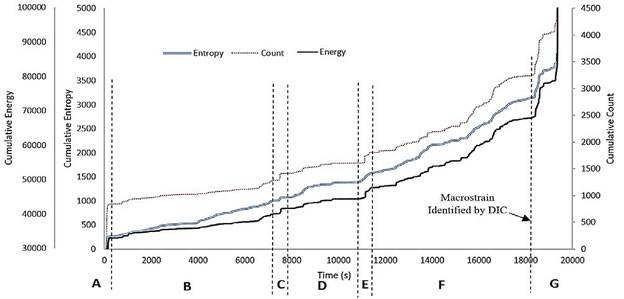
Bild 9 zeigt eine Darstellung der kumulativen Anzahl, der kumulativen Energie und der kumulativen Entropie über die gesamte Länge des zweiten Tests. Wie beim ersten Test ist aus der Grafik ersichtlich, dass alle Kurven den gleichen Trend aufweisen. Eine signifikante Zunahme der kumulativen Parameter im Bereich A ist auf die elastisch-plastische Umwandlung und das mechanische Rauschen zurückzuführen, das durch den Metall-Metall-Kontakt an den Probenhaltern verursacht wird. Die Schadensakkumulationsstufe in Region B geht einher mit einer minimalen Erhöhung der kumulativen Parameter. Ein starker Anstieg der kumulativen Parameter in Region C und E kann mit der Koaleszenz und dem Wachstum von Mikrorissen in Verbindung gebracht werden, während ein stabiler Anstieg der kumulativen Parameter in Region D und F auf eine stabile Anhäufung von Mikrorisswachstum im Material zurückzuführen ist. Nach Beginn der Makrodehnungslokalisierung beginnt der Makroermüdungsriss, der mit einem starken Anstieg der kumulativen Parameter einhergeht. Dieser Trend steht auch im Einklang mit anderen Untersuchungen [6][7]. Nach der Makro-Ermüdungsrissinitiierung zeigen die kumulativen Parameter eine stabile Variation zwischen 18.700 s und 19.300 s. Dieser Bereich ist mit einer stabilen Makro-Rissübertragung verbunden. Der stabile Anstieg der kumulativen Parameter aufgrund der stabilen Ausbreitung von Makro-Ermüdungsrissen steht auch im Einklang mit anderen Forschern [6][7][21]. Der starke Anstieg des kumulativen Parameters am Ende, nach 19.300s, ist auf eine instabile Rissausbreitung zurückzuführen, die von [6][7][7][21] vorgeschlagen wird.
Bild 9: Kumulative Entropie, kumulative Energie und kumulative Anzahl über die Zeit
© Farhan Tanvir et al, CC BY 4.0
4. Schlussfolgerung
In dieser Veröffentlichung wurde die Verwendung eines neuen qualitativen Parameters namens Schallemissions-Entropie, basierend auf der Renyi-Entropie vorgeschlagen. Der neue Parameter erwies sich als wirksam bei der Unterscheidung verschiedener Schadensphasen während eines Ermüdungs-Dauertests, was zum endgültigen Versagen von Edelstahl 316L (Werkstoff-Nummer 1.4404) führte. Die Schallemissions-Entropie ist ein Maß für die Unsicherheit der Amplitudenverteilung der Wellenform. Dadurch ist sie unabhängig von zeitabhängigen Parametern und Schwellenwerten. Aus den Ergebnissen dieser Experimente lässt sich folgendes schließen:
- Ein Vergleich zwischen der Schallemissions-Entropie und traditionellen Schallemissions-Spitzenamplitudenmessungen ergab, dass der anfängliche Anstieg der Spitzenamplitude des Signals als Folge der elastischen zu plastischen Umwandlung und des mechanischen Rauschens mit einem niedrigeren Wert der Schallemissions-Entropie verbunden ist. Wachstum und Koaleszenz von Mikrorissen, Makrorisseninitiierung, Makrorissenausbreitung und endgültigem Versagen sind mit einem höheren Entropiewert verbunden. Dies könnte eine effektive Methode zur Charakterisierung von Schäden im Material sein.
- Die kumulative Schallemissions-Entropie, die kumulative Anzahl und die kumulative Energie folgten dem gleichen Trend während des Ermüdungs-Dauertests mit Edelstahl 316L (Werkstoff-Nummer 1.4404). Die traditionelle kumulative Schallemissions-Analyse basierend auf Anzahl und Energie während der Ermüdung kann durch Schallemissions-Entropie ersetzt werden, da sie unabhängig von zeitabhängigen Parametern und Schwellenwerten ist.
Danksagung
Die Veröffentlichung der englischen Originalfassung dieser Publikation wurde durch die Unterstützung der London South Bank University und der Lloyd's Register Foundation ermöglicht, einer gemeinnützigen Stiftung, die durch die Unterstützung von ingenieurwissenschaftlicher Ausbildung, öffentlichem Engagement und der Anwendung von Forschung zum Schutz von Leben und Eigentum beiträgt. Die Arbeiten wurden durch das National Structural Integrity Research Centre (NSIRC) ermöglicht und dort durchgeführt, eine postgraduale technische Einrichtung für industriegeführte Forschung zur strukturellen Integrität, die vom TWI über ein Netzwerk von nationalen und internationalen Universitäten eingerichtet wurde und verwaltet wird.
10. Englische Veröffentlichung
Stephan Kallee übersetzte den unter einer Creative Commons Lizenz lizensierten Open-Access-Artikel am 10. Dezember 2018 vom Englischen ins Deutsche.
Der englische Open-Access-Artikel (Bild 10) wurde unter einer Creative Commons Lizenz (Namensnennung 4.0 International, CC BY 4.0) wie folgt veröffentlicht:
Farhan Tanvir, Tariq Sattar, David Mba , Graham Edwards, Elvin Eren and Yoann Lage:
MATEC Web Conf.
Volume 165, 2018
12th International Fatigue Congress (FATIGUE 2018)
Published online: 25 May 2018
DOI: 10.1051/matecconf/201816522007
Jede weitere Verbreitung dieses Werkes muss die Autoren sowie den Titel des Werks, die Zeitschrift und den digitale Objektbezeichner (DOI) aufführen.
Bild 10: Konferenz, Autoren, Zugehörigkeit, Titel und Englische Zusammenfassung
© Farhan Tanvir et al, CC BY 4.0
11. Einzelnachweise
1. C.J. Hailer, Handbook of Nondestructive EvaluationChapter 10,( The McGraw-Hill Companies, 2001).
2. M. David, R.B.K.N. Rao, Shock and Vibration Digest, 38, 3-16, (2006).
3. C. Boller, Sixth European Workshop on Structural Health Monitoring, (Dresden 2012).
4. A.C.E. Sinclair, D.C. Connors, C.L. Formby, Material Science and Engineering, 28, 263-273, (1977).
5. R. Roy, N. Parida, S. Sivaprasad, S. Tarafder. K.K. Ray, Meterial Science and Engineering A, 486, 562-571, (2008).
6. Z. Han, H. Lou, J. Cao and H. Wang, Materials Science and Engineering A, 528, 7751– 7756, (2011).
7. Z. Han, H. Luo, Y. Zhang and J. Cao, Materials Science & Engineering A, 559, 534-542, (2012).
8. H. Zhiyuan, L. Hongyun, S. Chuankai, L. Junrong and P. Mayorkinos, Material Science & Engineering A, 597, 270-278, (2014).
9. D.G. Aggelis, E.Z. Kordatos and T.E. Matikas, Mechanics Research Communication, 38, 106-110, (2011).
10. T.M. Roberts, M. Talebzadeh , Journal of construction steel reserach, 59, 679-694, (2003).
11. C. Mengyu, Z. Zhang, D. Quan and Y. Song, International Journal of Fatigue, 109, 145-156, (2018).
12. C. Mengyu, Z. Zaoxiao and D. Quan, Mechanical sytems and signal processing, 100, 617-629, (2018).
13. A. Renyi, Proc. of the 4th Berkeley Symp. Math. Statist. Prob, 1, 457-561, (1960).
14. D. Xu and E. Deniz, Information Theoretic Learning (47-102, New York, NY: Springer, 2010).
15. Gray. M, Robert. Entropy and Information Theory, (Boston, MA: Springer, 2011).
16. K. Ekˇstein, T. Pavelka, In Proceedings of PhD Workshop Systems & Control, University of West Bohemia, (2004).
17. A. Vahaplar,C.C. Celikoglu, M. Ozgoren, Mathematical and Computational Applications, 16,43-52, (2011).
18. V. Vijean, M. Hariharan, S. Yaacob, M. Nazri, B. Sulaiman and A. Adom, Computers and Electrical Engineering, 39,1549–1560, (2013).
19. V. Vijean, M. Hariharan, S. Yaacob, M. Nazri, B. Sulaiman, Biocybernetics and Biomedical Engineering, 34,169-177, 2014.
20. O. A. Amer, A.-L. Gloanec, S. Courtin, C. Touze, Procedia Engineering,66,651-660, (2013).
21. K.S. Han, K.H. Oh, Key Engineering Materials, 306-308, 271-278, (2006).
22. M. Chai, Z. Zhang, Q. Duan and Y. Song, International Journal of Fatigue, 109, 145-156, (2018).
23. D. Barktova, F. Vlasic, P. Mazal and O. Dvoracek, In Metal 23rd International Conference on Metallurgy and Materials, 1-6 (2014).
24. P. Mazal, F. Vlasic and V. Koula, Procedia Engineering, 133, 379-388, (2015).
25. M. Chai, J. Zhang, Z. Zhang, Q. Duan, G. Cheng. Applied Acoustics, 126, 101-113, (2017).

Diese Veröffentlichung ist unter der Creative-Commons-Lizenz „Namensnennung 4.0 International“ (CC BY 4.0) lizenziert.